Текстовые Задачи
План:
1.Моделирование реальных процессов.
2.Различные классификации текстовых
задач и систематизация методов и приемов их решения.
3.Решение текстовых задач составлением
уравнений и неравенств, систем уравнений и неравенств.
1) Построение математической модели. На этом этапе задается некоторый
«нематематический» объект — явление природы, конструкция, экономический
план, производственный процесс и т. д. При этом, как правило, четкое
описание ситуации на математическом языке затруднено. Поэтому сначала следует
выявить основные особенности явления и связи между его элементами на
качественном уровне. Затем найденные качественные зависимости формулируются на
языке математики, то есть строится математическая модель.
2) Решение математической задачи, к которой приводит построенная
модель. На
этом этапе большое внимание уделяется разработке алгоритмов и методов решения
задачи, при помощи которых может быть найден искомый результат.
3) Интерпретация полученных следствий из математической модели и её
исследование. Следствия, выведенные из модели на языке математики, интерпретируются на
языке, принятом в области применения данной задачи. Осуществляется поиск
количества возможных случаев решения задачи, при которых её решение будет иметь
или не иметь смысл.
4) Проверка адекватности модели. На этом этапе выясняется, согласуются
ли результаты эксперимента с теоретическими следствиями из модели.
Некоторые классификации текстовых
задач:
а)
Классификация задач по методу их решения;
б) Классификация задач по числу
действий;
в)
Классификация задач по содержанию (фабуле);
г)
Классификация задач по типу соответствующего уравнения.
Арифметический способ
решения задач: методы решения и разбора задач:
Синтетический метод
Этот метод заключается в
том, что разбор задачи начинают, исходя из известных данных в задачах. Выделяют
два известных данных и к ним подбирают вопрос. Затем снова выделяют два
известных данных и к ним подбирают вопрос. Так поступают до тех пор, пока не
ответят на вопрос задачи. С помощью синтетического приема разбора задач
осуществляется разбиение задачи на части, т.е. на простые задачи (решаемые
одним действием). Таким образом, осуществляется анализ; последовательное
решение всех простых задач есть синтез.
Задача: Расстояние между городами А и В равно
450 км .
Из А в В вышла грузовая машина. Два часа спустя, навстречу ей из В вышла
легковая машина. Скорость грузовой машины 60 км/ч , а скорость
легковой в 1,5 раза больше. Через сколько часов после своего выхода легковая
машина встретит грузовую?
Схема синтетического приема
разбора задач.
|
Знаем
|
Можно узнать
|
Каким действием найти?
|
|
Скорость грузовой
машины и сколько часов шла грузовая машина до выхода легковой
|
Сколько км прошла
грузовая машина до выхода легковой
|
60×2=120(км)
|
|
Расстояние между
городами и сколько км прошла грузовая машина до выхода легковой
|
Сколько км было между
машинами в момент выхода легковой машины
|
450-120=330(км)
|
|
Скорость грузовой
машины и во сколько скорость легковой больше скорости грузовой
|
Скорость легковой
машины
|
60км/ч×1,5=90(км/ч)
|
|
Скорость грузовой
машины и скорость легковой
|
Скорость сближения
грузовой и легковой машин
|
60+90=150(км)
|
|
Расстояние между
машинами в момент выхода легковой машины и на сколько км в час машины сближались (скорость сближения)
|
Через сколько часов
после выхода легковая машина встретит грузовую машину
|
330км: 150км/ч=2,2ч
|
Аналитический метод
Метод заключается в том,
что разбор начинают с вопроса задачи, т. е. исходят от неизвестного. К
неизвестному ставят вопрос и подбирают два данных, из которых одно данное или
оба данные смогут быть неизвестными. Затем снова к неизвестному ставится вопрос
и подбирают два данных, из которых одно или оба смогут быть неизвестными. Так
поступают до тех пор, пока оба данных будут известны. Тогда разбор задачи
заканчивается. С помощью аналитического приема осуществляется разбиение задачи
на части.
Схема аналитического
приема разбора задачи.
|
Чтобы узнать
|
Надо определить
|
Каким действием найти
|
|
Через сколько часов
после своего выхода легковая машина встретит грузовую машину
|
1.
Расстояние между машинами
2.
Скорость сближения
|
330км: 150=2,2(ч)
|
|
Чтобы найти расстояние
между машинами
|
1.
Расстояние между городами.
2.
Сколько км прошла грузовая машина до выхода легковой.
|
450км-120км=330(км)
|
|
Чтобы найти, сколько км
прошла грузовая машина
|
1.
Скорость грузовой машины
2.
Время движения грузовой машины
|
60км/ч×2ч=120(км)
|
|
Чтобы найти скорость
сближения
|
1.
Скорость легковой машины
2.
Скорость грузовой машины
|
90+60=150(км)
|
|
Чтобы найти скорость
легковой машины
|
1.
скорость грузовой машины
2.
во сколько раз скорость легковой больше
|
60×1,5=90(км/ч)
|
Аналитико-синтетический
метод
Метод заключается в том,
что разбор задачи начинают с помощью аналитического приема, ставят 1-2 вопроса
к неизвестному, подбирают данные. Когда становится ясным разбиение задачи на
части(на простые задачи) тогда применяют синтетический прием разбора и т.д.
Метод вспомогательных задач
Этот метод заключается в
том, что сначала решается задача с конкретными данными, осмысливается план
рассуждения, а затем этот план применяют к более сложным задачам или к задачам
более общего характера.
Пример: Имеющийся запас топлива составляет 80% того,
что потребуется в текущем году. На сколько % надо увеличить имеющийся запас
топлива, чтобы полностью можно было обеспечить потребности?
Перед решением этой задачи
рассматривается
вспомогательная задача:
Школа получила 500 учебников вместо 800 учебников, которые
потребуются в учебном году. На сколько % надо увеличить число учебников
математики?
1.
На сколько экземпляров надо
увеличить число учебников математики?
800-500=300(учебников)
2.
Сколько % составляет увеличенное количество книг по отношению к имеющимся?
300/500×100%=60%.
Затем решается основная
задача.
На какую часть надо
увеличить имеющийся запас топлива?
1-0,8=0,2(части)
На сколько % надо
увеличить имеющийся запас топлива?
0,2/0,8 ×100%=25%
Алгебраический метод
Алгоритм решения задач на процессы
1. Выяснить, о каких процессах
идет речь в условии задачи.
2. Выяснить, какими величинами
характеризуется каждый процесс.
3. Определить, какие из величин, характеризующих
процесс, известны (постоянные), а какие – не известны (переменные).
4. Обозначить величины процесса переменными.
5.
Установить зависимость между величинами в одном процессе (составить уравнение или неравенство)
6. Установить связь между
величинами в различных процессах (составить уравнение или неравенство).
7. Решить уравнения (неравенства) или
систему уравнений или неравенств.
Приведем пример задач, разных по фабуле, но имеющих
одинаковое решение.
Задача 1:
Два пешехода вышли одновременно навстречу друг другу из пунктов A и B и встретились через 6 часов.
За какое время пройдет это расстояние каждый из них, если первый может пройти расстояние между A и B на 5 часов быстрее.
|
Процесс
|
Скорость процесса
|
Время процесса
|
Результат процесса
|
Уравнение
|
|
Движение 1 пешехода
|
Vп1
|
t1 = 1/ Vп1
|
1
|
|
|
Движение 1 пешехода
|
Vп2
|
t2 = 1/ Vп2
|
1
|
|
|
Движение навстречу друг другу
|
Vп1 + Vп2
|
t
= 1/ (Vп2
+Vп1 )
|
1
|
1/
(Vп2
+Vп1 ) = 6
|
|
|
|
|
|
1/
Vп1 - 1/ Vп2 = 5
|
Задача 2:
Двое рабочих могут выполнить
работу за 6 часов. За какое
время может выполнить эту работу каждый из них, работая отдельно, если
один из них может выполнить всю работу
на 5 часов быстрее, чем другой.
|
Процесс
|
Скорость процесса
|
Время процесса
|
Результат процесса
|
Уравнение
|
|
Работы 1 рабочего
|
V1
|
t1 = 1/ V1
|
1
|
|
|
Работы 2рабочего
|
V2
|
t2 = 1/ V2
|
1
|
|
|
Движение навстречу друг другу
|
V1 + V2
|
t
= 1/ (V2 +V1 )
|
1
|
1/
(V2 +V1 )= 6
|
|
|
|
|
|
1/
V1 - 1/
V2 = 5
|
Графический метод
Пример: Два пешехода одновременно выходят навстречу друг другу из пунктов А и В и
встречаются через полчаса. Продолжая движение, первый прибывает в В на 11 мин
раньше, чем второй в А. За какое время преодолел расстояние АВ каждый пешеход?
В
прямоугольной системе координат строятся
графики движений двух пешеходов (считается, что они двигаются с
постоянными скоростями). На чертеже точки пересечений графиков соответствуют
встрече объектов в какой-то момент времени. Для любой точки А графика с координатами (x;y), x – это момент
времени, в который объект находится на расстоянии y от начальной точки.
Решение:
Пусть
p(x) –
зависимость пройденного первым пешеходом пути от времени х, q(x) –вторым
пешеходом. Построим графики этих соответствий на координатной плоскости.
Время,
за которое первый пешеход пройдет путь АВ
равна длине отрезка AG=BC; а время, затраченное вторы
пешеходом на этот же путь равно длине отрезка AD . Таким
образом, задача сводится к нахождению длин отрезков ВС и AD.
Треугольники
ВСО и DAO подобны
по трем углам. Из подобия следует следующее равенство:
Треугольники
DОE и BOF подобны
по трем углам. Из подобия следует следующее равенство:
(2)
Из
(1), (2) следует:
30(41+х)=(30+х)(х+11),
1230+30х=х2+41х+330,
х2+11х-900=0
ВС=30+25=55
(мин); AD=30+25+11=66
(мин).
Ответ:
55 мин, 66 мин.
Решение задач
различными способами.
Задача 1
Грибник и рыболов находятся на
расстоянии 220 м
от охотника и движутся в одном направлении с постоянными скоростями. Когда
охотник догнал грибника, рыболов отставал от них на 180 м . На каком расстоянии от
рыболова был грибник, когда охотник догнал рыболова?
Приведем три решения
этой задачи.
Решение 1(арифметическое)
Обозначим через voр – скорость сближения охотника и рыболова, через voг – скорость сближения охотника с грибником. Сначала рассмотрим движение с
момента, когда охотник был на расстояни
и
Теперь
рассмотрим движение с момента встречи охотника и рыболова. Когда охотник догнал
грибника, он преодолел разность расстояния между ними, т.е. искомое расстояние,
а также обогнал рыболова на 180
м . Таким образом, скорости voг соответствует искомый путь, а voр – равный 180 м . Таким образом, когда
охотник догнал рыболова, рыболов и грибник были на расстоянии .
Ответ: 99 м .
Решение 2 (алгебраическое)
. За это время рыболов и грибник прошли соответственно
, количество
пути, после чего расстояние между ними было
, что по условию равно 180 м . Таким образом,
получили уравнение:
(1)
Рассуждая
аналогичным образом, получаем, что расстояние между рыболовом и грибником в
момент, когда охотник догнал рыболова, была равна
(2). Из
уравнения (1) выражаем vp:
, - и подставляем его значение
в выражение (2) :
(м)
Ответ: 99 м .
Решение 3 (с помощью графиков)
В
прямоугольной системе координат построим
графики движений грибника, рыболова и охотника (считаем, что они идут с
постоянными скоростями). На чертеже точки пересечений графиков соответствуют
встрече объектов в какой-то момент времени. Для любой точки А графика с координатами (x;y), x – это момент
времени, в который объект находится на расстоянии y от начальной точки. В данной задаче за начальную
возьмём точку, в которой находился охотник, когда был на расстоянии 220 м от рыболова и грибника.
Здесь OA=220 м, CD=180 м, BE – искомый отрезок, обозначим
его через x. Рассмотрев две пары подобных
треугольников (OAC и EBC, BAE и CAD), получаем уравнения:
Сложив
эти уравнения, получим:
Ответ: 99 м .
Кратко графическое
решение будет иметь следующий вид:
Откуда x = 99 .
Использование неравенств при решении текстовых
задач
Задача 1
В математическом кружке число девочек больше 40%, но меньше
50% от всех участников. Какое наименьшее число участников кружка может быть при
этих условиях?
Решение:
Пусть в математическом
кружке х девочек, z мальчиков, тогда
.
Очевидно, что х = 3, z = 4 – наименьшие натуральные,
удовлетворяющие неравенству.
x+ z = 7, всего 7 человек в кружке.
Ответ:
7 человек.
Задача 2.
Прибывших на парад солдат планировали построить так, чтобы в
каждом ряду стояло по 24 человека. По прибытии оказалось, что не все солдаты
смогут участвовать в параде, и их перестроили так, что число рядов стало на 2
меньше, а число человек в ряду – на 26 больше нового числа рядов. Сколько
солдат прибыло на парад, если известно, что если бы все они участвовали в параде то, роту можно было бы перестроить
так, чтобы число рядов было равно числу человек в ряду?
Решение
Обозначим первоначально предполагавшееся число рядов за
N, тогда число
прибывших солдат будет равно 24N. После перестройки число рядов стало равным N-2, а число человек в ряду, большее
числа рядов на 26, соответственно N+24. Число солдат после перестановки
меньше, чем число прибывших первоначально. Зная, что число солдат после
перестроения будет (N-2)(N+24), запишем неравенство
24N > (N - 2)( N+24), равносильное следующему: N2-2N-48<0.
Решая его, получим, что число рядов, лежит в интервале
(-6;8). Число рядов N может быть лишь целым и положительным, т.е. возможно всего семь целых чисел от 1 до 7. Следует
учесть и сообщение о построении роты «квадратом» (число человек равно числу
рядов), первоначальное число солдат 24N должно быть полным квадратом. Но из
чисел от 1 до 7 последнему условию удовлетворяет лишь N =6. При этом число солдат равно 144.
Задача 3.
Токарю было поручено сделать 90 деталей, а ученику – 35.
Первые 30 деталей токарь делал с производительностью вдвое большей, чем ученик.
Известно также, что, изготовляя остальные 60 деталей, он делал еще на 2 детали
в час больше и закончил свою работу более чем на 1 час позже ученика. Однако
если бы токарь и первые 30 деталей делал с такой же производительностью, что и
оставшееся 60, то он закончил бы работу не ранее чем через 30 минут после
ученика. Какова производительность ученика?
Решение
Пусть Х > 0 – производительность ученика
(скорость работы). Тогда
.
Первое неравенство
приведем к виду , и получим,
что 4 ≤ Х ≤ 5 (1).
Второе неравенство
приводится к виду, что дает
5 ≤ х ≤ 14 (2).
Из неравенств
(1) и (2) следует x = 5
Нестандартные задачи
Задача 1
В двух
бригадах более 27 человек. Число членов первой бригады более чем в два раза превышает
число членов второй бригады, уменьшенное на 12. Число членов второй бригады
более чем в 9 раз превышает число членов первой бригады, уменьшенное на 10.
Сколько человек во второй бригаде?
По условию задачи: x+y>27
x/2>y-12
y/9>x-10
Этим трем неравенствам удовлетворяют координаты точек
заштрихованной области, без границы. Этой области принадлежит только одна точка с целыми координатами (11; 17)
Во второй бригаде 17 человек.
Ответ: 17 человек
Задача 2
Спортсмен
должен был выйти из дома в 7 часов 30 минут, сесть в ожидавшую его машину и
доехать на ней до стадиона к определённому моменту. Однако он вышел из дома в 5
часов 40 минут и побежал в противоположном направлении. Машина в 7 часов 10
минут отправилась от дома вслед за ним и, догнав спортсмена, доставила его на
стадион с опозданием на 10 минут. Во сколько раз скорость машины превышала
скорость бегущего спортсмена?
1)
О(5
ч 40 мин,) R(7 ч 30 мин), OR=110
2)
∆TDK– равнобедренный (т.к. скорость автомобиля
постоянная)
3)
ta = TQ=QK=15
мин, QR=5
мин, tc = OQ=105
мин. Расстояние QD
автомобиль прошел за 15 мин, а спортсмен – за 15
4)
Ответ: 7 раз.
Задача 3
Для того,
чтобы успеть на последний электропоезд, семье из 4- х человек нужно пройти по
пешеходному мосту. Одновременно по мосту
могу идти не более двух человек, причем в виду темного времени суток,
непременно, с фонариком. Если мост проходят двое, то они двигаются со скоростью
того, кто идет медленнее. За какое минимальное время пройдут мост все члены семьи, если известно,
что в одиночку Юра может пройти этот
мост за 2 минуты, Катя – за 4 минуты,
Игорек – за 10 минут, а Мария Ивановна –
за 16
минут? Фонарик у семьи только один.
Решение
Типичный неправильный ответ– в качестве
«сопровождающего» выбирается Юра, как самый быстрый. Тогда как стратегия «быстрый – с быстрым», «медленный – с медленным» приводит к правильному ответу: Юра и Катя -
4 мин, Катя - 4 мин, Игорек и
Мария Ивановна - 16 мин, Юра – 2 мин,
Юра и Катя 4 мин. Всего 30 мин.
Задача 4
Три хозяйки
приготовили одинаковые обеды, каждая для своей семьи, на общей печке. Первая
положила в топку 3 полена, вторая - 5 , а третья, не имевшая поленьев,
предложила им 80 рублей. Как по справедливости хозяйки должны разделить эти
деньги, если дрова прогорели полностью
1) 30 и 50
рублей; 2)20 и 60 рублей; 3) 10 и 70 рублей; 4)
40 и 40 рублей;
5) 5 и 75
рублей.
Решение
Типичный неправильный ответ, «изюминка» в том, что две хозяйки с поленьями
тоже их использовали и должны получить деньги только за неиспользованные
ими поленья*. 8/3 полена требуется на
приготовление одного обеда, что стоит 80 рублей, следовательно, одно полено
стоит
30 рублей: (80: 8/3= 30), тогда первой хозяйке нужно
отдать
30·3 - 80=10(рублей), а второй – 50·3 – 80
=70(рублей).
* Все 8
поленьев разделим на 3- это число
одинаковых обедов. Тогда на каждый обед нужно использовать 8/3 полена, а т.к. у третьей хозяйки не было
поленьев, то она заплатила за 8/3 полена 80 рублей. Отсюда находится стоимость
одного полена.













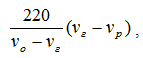














Комментарии
Отправить комментарий